Writing Scripts: Be prepared for all that the classroom throws at you!

Hi everyone!

Welcome to another weekly blog post from yours truly! Last week in my Math Teaching course, we learned about writing scripts for different parts of our lesson plan. Have you ever had an idea for a lesson activity or assignment, but felt unsure of how it would play out within the classroom? Would your students like the activity? Would it be too challenging or too easy? If it was too challenging, what guiding questions would you ask, in order to provide some clarity and understanding to your students? If it was too easy, how would you extend the activity to accommodate students who excel in this task?

As you look over your lesson plan for the day, you will be able to highlight the areas that you feel a little uncertain about implementing within the classroom. Speaking for myself, I know that I have trouble sleeping at night when I become anxious about not knowing how to handle the unexpected. In order to avoid the anxiety, I plan. I love planning because it gives me a sense of calm knowing that I am prepared for the unexpected. After I plan, I feel like I am ready to take on any challenge that is thrown my way because I have planned for it or something similar. Obviously, you are not able to plan for every single detail within your lesson because life is never that is easy. The beauty of teaching is that learning is spontaneous and each student's thought process and understanding is unique. Therefore, none of our lessons are going to turn out exactly the way we planned them, and that is great! It does make it easier on our nerves though, when we brainstorm possible scenarios that could arise during a particular activity or lesson, in order to create a general plan if students require additional support or extensions.

A few weeks ago, my partner and I created a math lesson plan that focused on Grade 9 Measurement in an applied level classroom. We designed a math center activity that allowed students to measure composite figures to find perimeter and area in a variety of different ways. One of our math center stations was tangrams (small shapes that make up a larger square). These tangrams can be used to create a number of different figures, such as a chair, boat, rocket, plane, etc.. We chose to have students work with a chair and a boat. They would need to use a ruler to measure the figure, in order to find the area and perimeter of their given composite shape. My partner and I realized that this
activity would be the most difficult for students to work with, so we decided to base our script off of this section of our lesson. Below is our script:

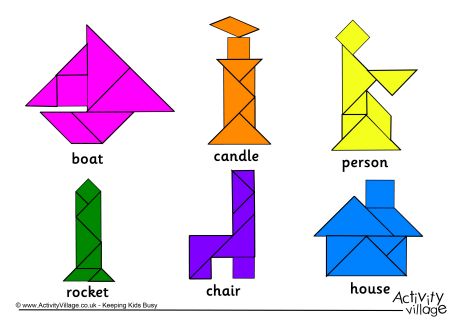Different Composite Figures
made from Tangrams

Lesson Plan Script

*see that group is struggling and has not started*

Teacher:  Hey guys, how’s it going?

Students murmur

Teacher: Do you guys know what you are looking for?

Student 1: Not really

Teacher: Okay, let’s look at the question and read it out loud. What is it asking you for?

Student 2:  We have to choose one of these shapes

Teacher: Perfect! Which one would you like to choose?

Student 1: I choose the boat!

Student 2: I kind of wanted to do the chair though…

Student 1: But boats are cool

Student 2: But the chair looks smaller

Student 1: I’ll do it if it’s easier

Teacher: Alright so we’re doing the chair. Now what do we need to do with the chair?

Students are silent in thought.

Teacher: Why don’t we look back at the question, and see what we need to do next?

Student 1: It says we need to find perimeter and area

Teacher: Okay. Which one would you like to work on first? Perimeter or area?

Student 2: Let’s do perimeter

Teacher: Alright, what information do we need to find perimeter?

Student 1: We need the side lengths. But there aren’t any lengths given.

Teacher: Well there is something provided at this station to help you measure that.

Student 2 grabs the rulers.

Teacher: Why don’t you guys get started and I’ll be back to check on you after I check on your classmates?

*10 minutes later: Teacher returns to check back on the group after observing the other groups*

Teacher observes that the students have measured all the side lengths of each smaller shape in the tangram and are trying to add them up.

Teacher:  Hi guys, how is it going?

Student 1: Much better! We have all the side lengths and now we are adding them together.

Teacher: Alright, well which sides did you include?

Student 2: All of them!

Teacher:  Let’s step back from the problem for a second and talk about perimeter. What do you think of when you hear the word perimeter?

Student 1: Well, the perimeter of a property.

Student 2: Or like the perimeter of a room.

Teacher: Then how would you describe perimeter in your own words?

Student 2: Well it’s kind of like when you go around the edge of something

Student 1: Yeah you like measure around a shape.

Teacher: Alright, and back to this activity, what shape did you choose?

Student 1: We chose a chair.

Teacher: Why don’t you guys sketch the chair for me?

Students roughly draw out similar chair outline. Teacher interrupts at this point.

Teacher: Alright, so this is your chair. How would you measure the perimeter of this?

Student 1 gestures around the outer edge: We would sum up these sides.

Student 2: But what about the other sides from the original picture?

Teacher: Well, are they a part of the perimeter you guys just showed me?

Student 2: Well, yes we need all the sides.

Student 1: But they aren’t actually outside sides. Only the ones in this picture are actually the outside edges of the chair.

Student 2: Why are they there then?

Teacher: Well tangrams are just a puzzle game that uses these standard small shapes to make new ones, like the chair and boat pictures. We aren’t using the tangrams right now as a puzzle, instead we are using their shapes to understand composite shapes, which are shapes made up of smaller shapes. So what measurements would you include in your perimeter for the chair?

Student 1 circles the edges of the tangram chair to show that he would measure the outside of the shape.

Student 2 circles the edges of the tangram as well.

Teacher: That’s right. So why don’t you use those sides to solve the perimeter, and then work on finding the total area of the chair?

-End of script-

I found that writing a script for this portion of the lesson was really helpful because it allowed me to think of where students would have the most trouble in deciphering what was being asked of them, and the steps that they would take to complete the task. By examining the word choice in the instructions for the activity, it gave me the opportunity to see where students might struggle and construct some guiding questions to provide clarity. I think that I would use this "script writing" method when planning most of my lessons because it made me feel more relaxed and confident in my teaching ability when I was able to put myself in the students' perspective and examine the activity.

I hope you all found this helpful! Enjoy the rest of your day!

Sincerely,
Dayna

Who doesn't love a good math game?

Hi everyone!

Welcome to another math post! This week in lecture, my classmates and I got the opportunity to play with some interactive math games- both online and offline.

The first game that we played is called Hedbanz. This is a classic game that people play at family events, board game nights with friends, and office parties (I imagine)! However, my professor altered it to help students practice their knowledge of the different forms of quadratic equations.

At the beginning of class, my professor handed out the headbands to every student in the classroom. Each headband had a quadratic equation on it, written in factor form, vertex form, and standard form. We were not allowed to look at the equation on our own headband. The goal of the game was to pair up with a partner, and ask each other "yes" or "no" questions, in order to figure out the equation on our forehead.

My best friend (K) and I immediately paired together to tackle this challenge. We put on our headbands and quickly wrote down some questions before we approached each other:

1. Am I in standard form? No
2. Am I in factored form? Yes
3. Do I have a coefficient in front of my brackets? No
4. Do I have more than one odd root? No
5. Do I have an odd root? No
6. Do I have two even roots? Yes
7. Do I have one positive, and one negative root? Yes
8. Are my roots the same digit? No
9. The only thing left to guess were the digits of our roots.

Results: K won the match, but we both had a great time and shared a few laughs during the game!

Here is a cute picture of the two of us afterwards! (Please forgive my awful selfie skills):

Why did my teacher let us play Hedbanz instead of handing out a worksheet on the different forms of quadratic equations?

Simple. It all comes down to three words that ALL teachers love: engagement, interactivity, and creativity.

My professor could have easily given us a worksheet, so that we could practice identifying the different forms of equations, but it would not have been nearly as successful! Even though the Hedbanz game was not a typical mathematics game, it gave students the opportunity to use math terminology in their questions (roots, standard, factored, vertex form, coefficient, etc.), and there was no pressure to arrive at a quick solution. Each pair could ask as many or as little questions as they needed to figure out their equation, and they were able to create questions that would help them best understand the different aspects of their equation.

This game is a great way to assess how well the students can use prior knowledge, problem solving and reasoning to figure out their headband equation. This game could be used as a diagnostic assessment before starting a unit on quadratic equations, or it could be used as a formative assessment before a major assignment or quiz. As the teacher observes the game unfold, he/she could make notes on areas of strengths and improvement for the class.

How can we use this game in our classroom? 

Hedbanz is versatile game that can be used to practice/review a number of math concepts in a fun and engaging way for students! We used it to test our knowledge of quadratic equations, but it can also be used to test students knowledge/application/thinking/communication skills in regards to prime factors,  graphs of functions, exponents, factoring, and more! The possibilities are endless for this game. This is also a great for ELL (English Language Learners) because it gives them an opportunity to practice asking questions, using math terminology, and demonstrating their knowledge by applying it in a low-risk setting that removes some of the anxiety and pressure from participating in a larger group setting.

I hope that you all enjoy this wonderful game, and have a great week ahead!

Dayna

Which one doesn't belong?

Hi everyone!

So today I thought we could play a math game! It's called "Which one doesn't belong?"

Objective:

There are four shapes/numbers/letters/graphs shown below; find a reason why each of the four (numbers) does not belong with the other three.

Rules: 

1. Have fun!

2. Be creative!

3. Try to think outside of the box.

4. Your thinking does not always have to be related to math!

------------------------------------------------------------------------------------------------

Take a moment, and try to come up with your own guesses/rules for why 9 does not belong with 16, 25, and 43.

My thoughts: 

The digits that make up 16, 25 and 43 all add up to 7. (16=1+6=7; 25=2+5=7; 43=4+3=7). The digits of 9 do not equal 7, so it does not belong. 

My mom's thoughts:

9 is the only single digit number! 

Both answers are right because they both find a rule that groups 16, 25, and 43 together such that 9 does not belong in the group. Both answers are mathematical because they use math terminology such as "add", "number", "single", "digit(s)". And both answers discuss the different properties of numbers.

In my math teaching course, we were introduced to a website called "Which one doesn't belong?" (www.wodb.ca). It was created by a woman named Mary Bourassa who accepts entries, tests them to see if they fit the criteria, and then posts them on her website for people to solve.

I love this activity because of it's flexibility. This activity presents a puzzle for students to solve, using their prior knowledge and experiences to help them find patterns, create categories/groups, and form rules that each number must follow in order to be part of the group. It is also OPEN to possibility. As long as a student sees a pattern that can be proven, their answer is correct! This opens up the playing field for all students because there is no "right answer" or set formula that has to be followed to arrive at an answer. This game is about being creative, open-minded, and thinking outside of the box.

I tested this game out with my mom because I wanted to see if we would get any different answers by examining the problem from different perspectives. My mom used to be a banker, so she is very good with numbers, but she doesn't study math as a hobby. This offered a new perspective because she thought in terms of the operations (addition, subtraction, multiplication, etc.) between numbers, while I tried to find patterns between the digits of a number. We tried three different "Which one doesn't belong?" puzzles, and I found that sometimes we came up with the same rule or category for a group, while other times, we had completely different responses! I think this would be a great activity to do with a class as a warm up exercise because it allows the teacher to perform a quick diagnostic assessment to see where students are at in their learning, but it is also a great opportunity for students to learn from each other and see that a puzzle can have multiple solutions.

As an expansion, I thought that it might be a fun challenge for students to try to make their own "Which one doesn't belong?" puzzle, and either share it with their classmates to solve, or e-mail it to Mary Bourassa. If it is solvable and Ms. Bourassa is able to test it successfully, then it may be published on her website for other people from around the world to solve. How cool would that be?

That's it for now! I hope everyone has a great weekend!

Dayna

Open Questions = Open Access for all Students

Hi everyone!

In my Math Teaching course, we learned about the power of using open ended questions in the classroom.

Often times, students have a fear of math simply because they are worried that they will not be able to find the correct answer. Many students worry that they will be put on the spot in front of their teacher and peers, and they will be forced to admit that they "do not know the answer" or worse, attempt to provide a solution and realize it's the wrong answer. This fear of public humiliation can cause math anxiety that continues to build the longer that students feel like they have nothing meaningful to contribute to their class.

By starting a lesson with an open-ended question, all students are able to participate in the class discussion because there is "no right answer". As my teacher put it, "If I went around to each group, I know that every student in that group would have something to tell me about the picture/pattern/question." It would be amazing to design a question that can capture the attention of all of my students, so that they can all feel like they are a part of the discussion. By using open-ended questions at the beginning of a lesson, it gives students an opportunity to get into the flow of the class, gets them excited and engaged, and it eases some of their anxiety when they are able to play an active role in the classroom.

A great example of an open-ended math question is estimation. Estimation is a skill that students can develop to make accurate guesses that will help them determine if their solutions are realistic or completely off-base. Estimation can also be used in the real world. By helping our students develop their estimation skills, we are helping them determine if they have enough money to pay for their items when they are standing in the check-out lane; we are helping them determine if their furniture will fit into their college dorm room; we are helping them estimate how long it will take to walk home or drive somewhere; and we are helping them plan events when they need to estimate how much pizza needs to be ordered for a large number of people. This is a great tool to foster because it brings the real world into the math classroom, and it brings math into the real world.

We can use estimation as an open-ended question because every student has their own opinion and internal guesses; therefore, every student can participate in the lesson without fearing that their answers will be rejected. Estimations are accurate guesses; they do not always have to be exact, so this may ease some of the math anxiety associated with getting the correct answer.

A great resource for any teacher that would like to include estimation in their lessons, is Estimation180. It is a website that provides pictures and videos that students can watch/examine to make predictions; once they have all decided on an accurate guess, the teacher can show the answer image or video and students can compare their answers with the actual answer. The teacher can then have a follow-up discussion, where students can determine why their answer may have been a bit off. Here is a video example from Estimation180 that helps students begin to think about adding fractions:

For more fun ways to use estimation in your classroom, check out Estimation180.org. 

Thanks for reading everyone, and have a wonderful day!

Dayna

Yay for Manipulatives!

Hi everyone!

Today, I wanted to introduce the topic of manipulatives, and address some of the misconceptions that we may have around this subject. 

What are manipulatives? 

Manipulatives are tools that students can use to help them approach and solve math problems. They are concrete items that students can move and explore. Even though math is the "universal" language, sometimes it is difficult to understand or decipher, so students can use manipulatives to represent math in a new way that makes sense to them. 

What are some of the benefits of manipulatives? 

• Manipulatives decrease math anxiety because it offers students a concrete way to interact with abstract concepts 
• They are fun to explore! Math doesn't always need to be represented on paper!
• They can be used in all grade levels and streams. Yes, that's right; they can be used in both ACADEMIC and APPLIED. Manipulatives do not just apply to one particular stream or age group, since they can be used in Grade 12 and College/University. 
• They provide both a visual and kinesthetic approach to mathematics, so they are a great way to offer differentiated instruction to all learning types. 
• In order to save money and provide more manipulatives for your students to work with, you can make your own! 
• I was able to make my own algebra tiles by gluing a piece of red and blue construction paper together, and cutting it into different shapes (long, thin rectangles represent the x term; and small squares represent the constant term 1). This cost me a total of 60 cents, since I only used 4 sheets of construction paper.    

Construction paper Algebra Tiles

Algebra tiles can be used for a number of different algebraic concepts, such as factoring, adding and subtracting expressions, multiplying and dividing expressions, and completing the square! (Who knew!) I focused on using algebra tiles to collect like terms, which I have included in a video below. I hope this helps for anyone who is new to using algebra tiles! 

Are there any problems with manipulatives?

Personally, I don't see a problem with manipulatives because they allow students to learn at their own pace and discover new ways of representing and understanding mathematics. 

However, there tends to be a problem when students are unable to use them during a test, when they previously had access to them during lessons and homework sessions. I understand that teachers want to see if students are able to demonstrate their work using the abstract procedures shown in class, but how are students able to display this level of abstract thinking, when they need a concrete tool to help them understand? Tests already place a heavy amount of pressure on students, especially when these students have math anxiety. 

Taking away their manipulatives during a test, might be the equivalent of throwing them into an ocean without a life jacket. No wonder students have a growing fear of math. 

Some students will use their manipulatives during class in order to help them understand an abstract concept, but will no longer need them for the test because they have grasped the abstractness. However, others will depend on their manipulatives to help them through a stressful assessment; we should not be taking that away from them. I believe that a student should be able to use any strategy or tool to arrive at an answer, and they should not be penalized based on their chosen strategy. As long as students are able to express their answers and explain the procedure they used, then they have effectively demonstrated their learning. 

My final critique on manipulatives is that some teachers lack the training to use them in the classroom. Often times, the Ministry deems that manipulatives should be implemented in the classroom (which is great!), but they do not provide teachers with the proper training to effectively incorporate them in their lessons. This lack of training may cause confusion for students, frustration for teachers, and the benefits of manipulatives to not be reaped. I think that an easy fix to this potential problem would be to provide teachers with PD days that would help them learn more about the manipulatives, and provide examples and suggestions on how to use them in their lessons. 

Overall, manipulatives are a great tool for teacher's to have in their toolbox. We just need to know how to incorporate them in our lessons in order for them to be effective!

Thank you all for reading, and I hope you have a great day!

Dayna

The Skyscraper Challenge for all Ages!

Hi everyone!

Thanks for tuning into my first blog post. This week, in my Mathematics Teaching course for Intermediate/Senior, my professor sectioned us off into groups to complete the Skyscraper Challenge. For those of you who have never heard of this activity, I have provided a picture, as well as a video below to help you visualize.

In this activity, we used linking cubes to make towers. Since this is a 4x4 square we were only able to use linking cube towers in groups of 1, 2, 3, or 4. For all of you Sudoku lovers out there, this game is very similar because each row and column must have one set of 1, 2, 3, and 4 linking cube towers; repeats are not allowed. The numbers along the sides of the square represent how many "towers of linking cubes" you will be able to see when you look from that direction.

Before my class began the activity, we were given a limited amount of instruction, and we were not explicitly told what the numbers on the sides of the square represented. My group struggled for about 10-15 minutes on our own; we asked each other questions, tested out conjectures, and failed. We were stumped. Finally, we asked our teacher for a bit more guidance, and also looked to the internet as a resource, in order to help us find a clue to solve the puzzle. Once we discovered that we needed to be able to see a given number of "towers/buildings" from each square, we set off to solve the problem! It was fun and exciting to play around with the towers of linking cubes, in order to see what satisfied all of the requirements of the given puzzle. I felt myself smiling and laughing with my group, and I almost didn't want to stop when our teacher finally called our class in for a group discussion of the activity.

My teacher informed us that this activity was actually used in a grade 1 classroom to help them develop spacial reasoning. Some of you may be wondering how a grade 1 student, who is barely 6 years old, can solve a puzzle that is still challenging for university students. At first, I was questioning this too, but then I realized that sometimes, without meaning to, we can underestimate the capabilities of our students.

I remember when I was little, and being told that I was too young to do or learn something. My parents would tell me that I could do/learn this when I was older. I would badger them with questions like, "Why do I have to be older? How much older do I have to be? When exactly will you be able to tell me these things?" and as a last resort, when they still wouldn't give into me, I would use the, "I'm old enough now! I can understand things!" card. I was always frustrated when my age hindered me from learning news things, and I could not wait to be older!

I wonder if teaching is similar. My professor gave this activity to a grade 1 class, not knowing if they would be able to solve it or not. However, the results surprised her. She found that these students discovered solutions to the puzzle through play based learning. These students did not get frustrated by not knowing the answer, they just continued to try, play and learn. One of my peers from my English Teaching class brought up the point that we wait until students reach a certain age to teach them about new topics. In math, we deem that by grade 11, students will be capable of learning functions. What makes a grade 10 student different from a grade 11 student? One year? We believe that when students are 15, they are not ready to learn about functions, but when they turn 16, they have reached the perfect age. Is this right? Could it be that by waiting to teach students about these complex concepts, that we are reinforcing the giant learning gap that exists between each grade? What would happen if we introduced topics earlier? Would this help ease students anxiety over mathematics if they were exposed to these concepts at an earlier age, so that by the time that they reached the required age of learning, these concepts would already be familiar?

I know that I have raised a lot of questions that I don't necessarily have the answers to. However, I feel that this issue is something to consider. Sometimes, we do make assumptions about students based on their  age, grade level, or stream (academic, applied or locally developed). By giving students the opportunity to try activities that we feel may be above their grade level, we may be surprised by what we see. If we find that students are struggling to understand the concept, we can provide more scaffolding and guidance to help them along; however, if we notice that they are able to solve these problems on their own with very little assistance, our assumptions will no longer be valid. We need to give students a chance to try new things, in order to expose them to these concepts/strategies/ways of thinking earlier, so that their learning will be continuous and familiar, instead of abrupt, disconnected, and something to be feared.

If you would like to use the Skyscraper activity in your classroom, or would simply like to solve the puzzle yourself, there are daily puzzles available at the following link: https://www.brainbashers.com/skyscrapers.asp

Thank you all for reading, and have a wonderful day!

Dayna

Meet the Blogger

Hi everyone!

In case you are a little curious about the person behind the blog posts, I thought I would introduce myself!

My name is Dayna Perry and I am a math-fanatic. What can I say? I love the challenge of solving a math problem, and I live for the rush of excitement that comes from finding a solution (one of many, in some cases)! I am also a sucker for numbers, but even numbers are my favourite! I love Sudoku, nano-grams, and Reno-grams; basically any game that allows me to work and play with numbers has me fascinated! I will also apologize in advance for my overzealous use of exclamation marks in my writing. For some reason, exclamation marks tend to make everything seem more exciting, especially when placed at the end of a sentence relating to the topic of math. Math tends to be seen as a boring subject, so it couldn't hurt to throw a few exclamation marks in to help spice up this seemingly dull (never!) topic. Could it?

All joking matters aside, math is a wonderful subject. I have always enjoyed math, and have loved teaching others when they have struggled to understand some of the basic or more complex concepts. For this reason, I chose to pursue a career in math education. I am heading into my fifth and final year, which is also known as the year of teacher's college. This blog will be used as a tool to help me reflect on my math teaching experience. I hope to use this year to learn how to make math meaningful and relevant for my students, so that they will not have to ask me, "Ms. Perry, what is the point? Why am I learning this? When am I ever going to use this in the real world?". My mission throughout the year, and throughout my teaching career is to help students answer these questions on their own, by providing them with real world examples and applications. I want my students to have fun! Why is it acceptable for the math classroom to be boring? Math should never be boring...if it is, then we have a serious problem on our hands. I want to be able to restore some of the confidence that has been lost along the way for many of my students who believe in the stereotypical "math person/type". I need to help my students realize that we are all capable of learning math, and the true beauty of math is that it is universal; everyone can learn to understand it and find meaning in it.

Throughout this year of teacher's college I hope to make mistakes and learn from them. I hope that you will join me in my adventure, and hopefully we will be able to make mistakes together, and learn from one another! 

To end this post on a good note, here is a math joke for you to enjoy! 

+Dayna+